Jacobian curve
In mathematics, the Jacobi curve is a representantion of an elliptic curve different than the usual one (Weierstrass equation). Sometimes it is used in cryptography instead of the Weierstrass form because it can provide a defence against simple and differential power analysis style (SPA) attacks; it is possible, indeed, to use the general addition formula also for doubling a point on an elliptic curve of this form: in this way the two operations become indistinguishable from some side-channel information.[1] The Jacobi curve offers also faster arithmetic compared to the Weierstrass curve.
The Jacobi curve can be of two types: the Jacobi intersection, that is given by an intersection of two surfaces, and the Jacobi quartic.
Contents |
Definition: Jacobi intersection
Let  be a field. An elliptic curve in the projective space
be a field. An elliptic curve in the projective space 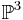 over
over  can be represented as the intersection of two quadric surfaces:
can be represented as the intersection of two quadric surfaces:
It is possible to define the Jacobi form of an elliptic curve as the intersection of two quadrics, using the following map applied to the usual Weierstrass curve 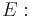
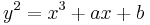 ,
, 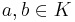 :
:
This map sends the point 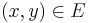 to the point
to the point 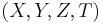 that satisfies the following system of equations:
that satisfies the following system of equations:
The map 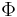 can be applied to an elliptic curve in the Weierstrass form
can be applied to an elliptic curve in the Weierstrass form 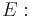
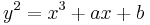 with three points of order two: this means that the polynomial
with three points of order two: this means that the polynomial 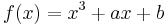 has three roots in the field
has three roots in the field  . Suppose that the roots are
. Suppose that the roots are 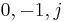 , with
, with 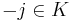 , then the three points of order two are: (0,0), (-1,0), (-j,0) and the curve
, then the three points of order two are: (0,0), (-1,0), (-j,0) and the curve  can, thus, be written as:
can, thus, be written as:
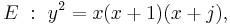
where 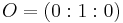 is the "point at infinity", that is the neutral element in the group law.
is the "point at infinity", that is the neutral element in the group law.
The curve  corresponds to the following intersection of surfaces in
corresponds to the following intersection of surfaces in 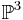 :
:
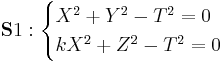 .
.
The "special case" is when j=0: the elliptic curve has a double point and thus it is singular.
S1 is obtained by applying to  the transformation:
the transformation:
 :
: 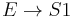
Group law
(See also The group law).
Given an elliptic curve, it is possible to do some "operations" between its points: for example one can add two points P and Q obtaining the point P+Q that belongs to the curve ; given a point P on the elliptic curve, it is possible to "double" P, that means find [2]P=P+P (the square brackets are used to indicate [n]P, the point P added n times), and also find the negation of P, that means find -P. In this way, the points of an elliptic curve forms a group. Adding and doubling formulas are useful also to compute [n]P, the nth multiple of a point P on an elliptic curve: this operation is considered the most in elliptic curve cryptography.
For S1, the neutral element of the group is the point 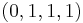 , that is the image of
, that is the image of 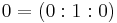 by
by  .
.
Addition and doubling
Given 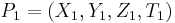 and
and 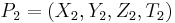 , two points on
, two points on 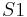 , the coordinates of the point
, the coordinates of the point 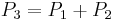 are:
are:
These formulas are also valid for doubling: it sufficies to have 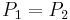 . So adding or doubling points in
. So adding or doubling points in 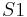 are operations that both require 16 multiplications plus one multiplication by a constant (
are operations that both require 16 multiplications plus one multiplication by a constant ( ).
).
It is also possible to use the following formulas for doubling the point 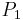 and find
and find ![P_3=[2]P_1](/2012-wikipedia_en_all_nopic_01_2012/I/930559a4e3b0c251dcb408df8e4336f9.png) :
:
Using these formulas 8 multiplications are needed to double a point. However there are even more efficient “strategies” for doubling that require only 7 multiplications.[2] In this way it is possible to triple a point with 23 multiplications; indeed ![[3]P_1](/2012-wikipedia_en_all_nopic_01_2012/I/7261ead98aa4e4c8e532cd1ca71b84f8.png) can be obtained by adding
can be obtained by adding 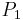 with
with ![[2]P_1](/2012-wikipedia_en_all_nopic_01_2012/I/1daaf3fc1b93cf1b3ae06c9fee7d4aa0.png) with a cost of 7 multiplications for
with a cost of 7 multiplications for ![[2]P_1](/2012-wikipedia_en_all_nopic_01_2012/I/1daaf3fc1b93cf1b3ae06c9fee7d4aa0.png) and 16 for
and 16 for ![P_1%2B[2]P_1](/2012-wikipedia_en_all_nopic_01_2012/I/4d29c621ecd7bcba2fd11bd0030c4f0e.png) [2]
[2]
Example of addition and doubling
Let the field 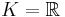 , or
, or 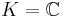 . Consider the case:
. Consider the case:
Consider the points 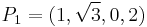 and
and 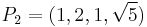 : it is easy to verify that
: it is easy to verify that 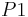 and
and 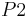 belong to S1 (it is sufficient to see that these points satisfy both equations of the system S1).
belong to S1 (it is sufficient to see that these points satisfy both equations of the system S1).
Using the formulas given above for adding two points, the coordinates for 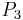 , where
, where 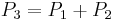 are:
are:
The resulting point is 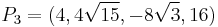 .
.
With the formulas given above for doubling, it is possible to find the point ![P_3=[2]P_1](/2012-wikipedia_en_all_nopic_01_2012/I/930559a4e3b0c251dcb408df8e4336f9.png) :
:
So, in this case ![P_3 = [2]P_1 = (0,12,-12,12)](/2012-wikipedia_en_all_nopic_01_2012/I/783e4b3951c326b1cee30602aef38b4e.png) .
.
Negation
Given the point 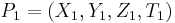 in
in 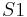 , its negation is
, its negation is 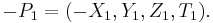
Addition and doubling in affine coordinates
Given two affine points 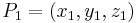 and
and 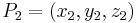 , their sum is a point
, their sum is a point 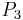 with coordinates:
with coordinates:
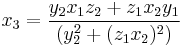
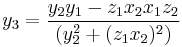
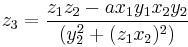
These formulas are valid also for doubling with the condition 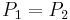 .
.
Extended coordinates
There is another kind of coordinate system with which a point in the Jacobi intersection can be represented.
Given the following elliptic curve in the Jacobi intersection form:
the extended coordinates describe a point 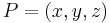 with the variables
with the variables 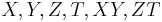 , where:
, where:
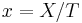
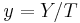
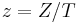
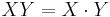
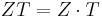
Sometimes these coordinates are used, because they are more convenient (in terms of time-cost) in some specific situations.
To have more information about the operations based on the use of these coordinates see http://hyperelliptic.org/EFD/g1p/auto-jintersect-extended.html
Definition: Jacobi quartic
Let  be a field. An elliptic curve in Jacobi quartic form can be obtained from a curve
be a field. An elliptic curve in Jacobi quartic form can be obtained from a curve  in the Weierstrass form with at least one point of order 2:
in the Weierstrass form with at least one point of order 2:
with 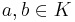 .
.
Let 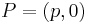 be a root of
be a root of 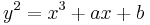 , then P is a point of order 2 of the elliptic curve; let
, then P is a point of order 2 of the elliptic curve; let 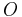 be the point at infinity.
be the point at infinity.
The following transformation  sends each point of
sends each point of  to a point in the Jacobi coordinates (
to a point in the Jacobi coordinates (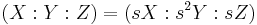 )
)
 :
: 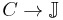
Applying  to
to  , one obtains a curve in
, one obtains a curve in 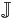 of the following form:
of the following form:
where 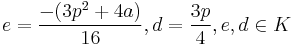 .
.
C' represents an elliptic curve in the Jacobi quartic form, in Jacobi coordinates.
Jacobi quartic in affine coordinates
The general form of a Jacobi quartic curve in affine coordinates is:
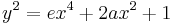 ,
,
where often 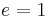 is assumed.
is assumed.
Group law
The neutral element of the group law of 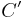 is the projective point
is the projective point 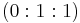 .
.
Addition and doubling in affine coordinates
Given two affine points 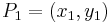 and
and 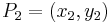 , their sum is a point
, their sum is a point 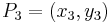 , such that:
, such that:
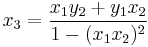
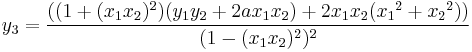
As in the Jacobi intersections, also in this case it is possible to use this formula for doubling as well.
Addition and doubling in projective coordinates
Given two points 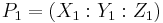 and
and 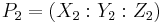 in
in 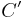 , the coordinates for the point
, the coordinates for the point 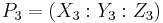 , where
, where 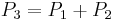 , are given in terms of
, are given in terms of 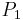 and
and 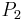 by the formulae:
by the formulae:
One can use this formula also for doubling, with the condition that 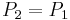 : in this way the point
: in this way the point ![P_3=P_1%2BP_1=[2]P_1](/2012-wikipedia_en_all_nopic_01_2012/I/70626eefc9d683c510b2578a7314e8c6.png) is obtained.
is obtained.
The number of multiplications required to add two points is 13 plus 3 multiplications by constants: in particular there are two multiplications by the constant  and one by the constant
and one by the constant  .
.
There are some "strategies" to reduce the operations required for adding and doubling points: the number of multiplications can be decreased to 11 plus 3 multiplications by constants (see [4] section 3 for more details).
The number of multiplications can be reduced by working on the constants  and
and  : the elliptic curve in the Jacobi form can be modified in order to have a smaller number of operations for adding and doubling. So, for example, if the constant
: the elliptic curve in the Jacobi form can be modified in order to have a smaller number of operations for adding and doubling. So, for example, if the constant  in C’ is significantly small, the multiplication by
in C’ is significantly small, the multiplication by  can be cancelled; however the best option is to reduce
can be cancelled; however the best option is to reduce  : if it is small, not only one, but two multiplications are neglected.
: if it is small, not only one, but two multiplications are neglected.
Example of addition and doubling
Consider an elliptic curve in the Weierstrass form in affine coordinates over the field 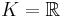 , or
, or 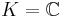 , with
, with 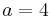 and
and 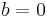 :
:
 has a point
has a point  of order 2:
of order 2: 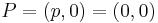 .
.
Applying the function  to
to  , the following elliptic curve in projective Jacobi quartic form is obtained:
, the following elliptic curve in projective Jacobi quartic form is obtained:
where 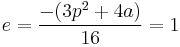 and
and 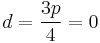 .
.
Choosing two points 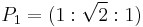 and
and 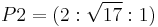 , it is possible to find their sum
, it is possible to find their sum 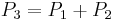 using the formulae for adding given above:
using the formulae for adding given above:
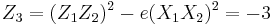 .
.
So 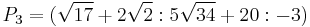 .
.
Using the same formulae, the point ![P_3=[2]P_1](/2012-wikipedia_en_all_nopic_01_2012/I/930559a4e3b0c251dcb408df8e4336f9.png) is obtained:
is obtained:
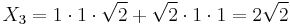
![Y_3 = [1%2B1\cdot1]\cdot[\sqrt{2}\cdot\sqrt{2}] %2B 2\cdot1\cdot(1^4%2B1^4) = 8](/2012-wikipedia_en_all_nopic_01_2012/I/4db0625465c86bf207095a1f59b0e238.png)
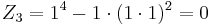
so, 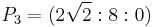 .
.
Negation
The negation of a point 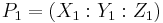 is:
is:
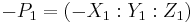
Alternative coordinates for the Jacobi quartic
There are other systems of coordinates that can be used to represent a point in a Jacobi quartic: they are used to obtain fast computations in certain cases. For more information about the time-cost required in the operations with these coordinates see http://hyperelliptic.org/EFD/g1p/auto-jquartic.html
Given an affine Jacobi quartic
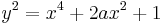
the Doubling-oriented XXYZZ coordinates introduce an additional curve parameter c satisfying
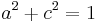
and they represent a point (x,y) as (X, XX, Y, Z, ZZ, R), such that:
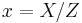
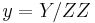
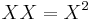
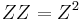
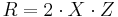
the Doubling-oriented XYZ coordinates, with the same additional assumption (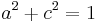 ), represent a point (x,y) with (X, Y, Z) satisfying the following equations:
), represent a point (x,y) with (X, Y, Z) satisfying the following equations:
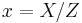
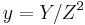
Using the XXYZZ coordinates there is no additional assumption, and they represent a point (x,y) as (X,XX,Y,Z,ZZ) such that:
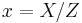
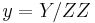
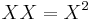
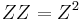
while the XXYZZR coordinates represent (x,y) as (X,XX,Y,Z,ZZ,R) such that:
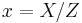
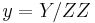
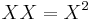
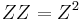
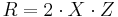
with the XYZ coordinates the point (x,y) is given by (X,Y,Z), with:
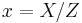
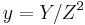 .
.
See also
For more information about the running-time required in a specific case, see Table of costs of operations in elliptic curves.
External links
Notes
- ^ Olivier Billet, The Jacobi Model of an Elliptic Curve and Side-Channel Analysis
- ^ a b P.Y.Liardet and N.P.Smart, Preventing SPA/DPA in ECC Systems Using the Jacobi Form, pag 397
- ^ a b Olivier Billet and Marc Joye, The Jacobi Model of an Elliptic Curve and Side-Channel Analysis, pag 37-38
- ^ Sylvain Duquesne, Improving the Arithmetic of Elliptic Curves in the Jacobi Model-I3M, (UMR CNRS 5149) and Lirmm, (UMR CNRS 5506), Universite Montpellier II
References
- Olivier Billet, Marc Joye (2003). The Jacobi Model of an Elliptic Curve and the Side-Channel Analysis. Springer-Verlag Berlin Heidelberg 2003. ISBN 978-3-540-40111-7. http://www.springerlink.com/content/p0013kgt6xpulkvb/fulltext.pdf.
- P.Y. Liardet, N.P. Smart (2001). Preventing SPA/DPA in ECC Systems Using the Jacobi Form. Springer-Verlag Berlin Heidelberg 2001. ISBN 978-3-540-42521-2. http://www.springerlink.com/content/h3bhhlxn9qbg05pj/fulltext.pdf.
- http://hyperelliptic.org/EFD/index.html
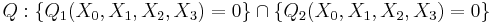
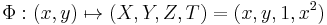
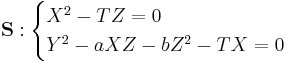
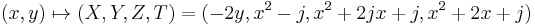
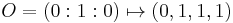
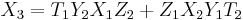
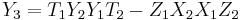
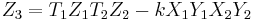
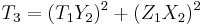
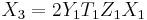
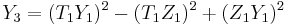
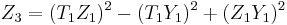
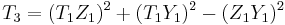
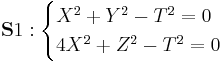
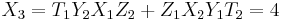
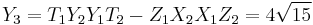
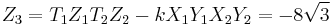
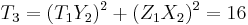
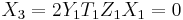
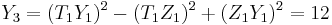
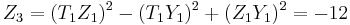
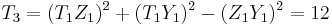
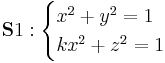
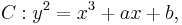
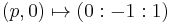
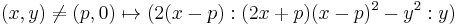
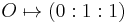
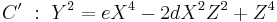
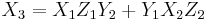
![Y_3 = [(Z_1Z_2)^2%2Be(X_1X_2)^2][Y_1Y_2-2dX_1X_2Z_1Z_2]%2B2eX_1X_2Z_1Z_2(X_1^2Z_2^2%2BZ_1^2X_2^2)](/2012-wikipedia_en_all_nopic_01_2012/I/09f5a122b8cc295fa6b7667aae6fb2d8.png)
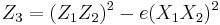
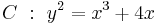
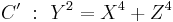
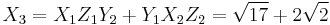
![Y_3 = [(Z_1Z_2)^2%2Be(X_1X_2)^2][Y_1Y_2-2dX_1X_2Z_1Z_2]%2B2eX_1X_2Z_1Z_2(X_1^2Z_2^2%2BZ_1^2X_2^2) = 5\sqrt{34} %2B 20](/2012-wikipedia_en_all_nopic_01_2012/I/6bd567e409915af38356413cc0edcdf1.png)